문제 링크: https://www.acmicpc.net/problem/5719
재밌는 문제입니다. 다익스트라 알고리즘을 응용해서 풀 수 있습니다.
알고리즘은 간단합니다
- 1. 다익스트라 알고리즘을 수행해서 최단경로 길이를 저장
- 2. 최단경로의 간선을 삭제
- 3. 다익스트라 알고리즘을 다시 수행
- 최단경로가 없으면 -1
- 최단경로가 있는데 길이가 그대로면 다시 2 -> 3 반복
- 최단경로 길이가 1.의 길이보다 적어지면 출력
별로 어려울 게 없습니다. 다익스트라 알고리즘에서 parent 배열만 만들어주면 될 듯 합니다. 그런데 제출해보면 틀렸다고 나옵니다.
문제는 최단경로의 간선을 삭제하는 부분에 있었습니다.

위 형태의 그래프가 있고 start=0, destination=2라고 하면 0-1-2, 0-3-2 둘 다 거리가 3으로 최단경로가 됩니다.

그런데 parent 배열을 사용해 하나의 최단 경로만 지우면 위 두 그래프 중에 하나의 모양이 나올 겁니다.
아래의 경우, 경로가 이어지지 않으니 답이 -1이지만, 위 그래프는 6이라는 값이 나옵니다. 3->2의 간선은 최단경로에 포함되는 간선이니 포함되면 안되는데 지워지지 않아 6이라는 오답이 나와버립니다.
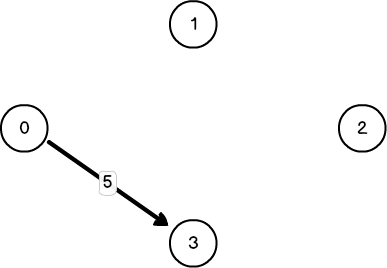
결국 이런식으로 Fig 1.에서 최단경로에 포함되는 간선들을 모두 지워줘야 한다는 것을 알 수 있습니다.
한 노드가 여러 부모가 있을 수 있으니 parent들의 인덱스를 저장해줘야 하고, 그리고 다익스트라 알고리즘 안에서 parent를 저장할 때 distance가 업데이트될 때 뿐 아니라 동일한 distance의 경우 parent 배열에 추가를 해줘야 합니다.
#pragma GCC optimize ("Ofast")
#define _CRT_SECURE_NO_WARNINGS
#define _SILENCE_CXX17_C_HEADER_DEPRECATION_WARNING
#include <bits/stdc++.h>
using namespace std;
const int INF = 987654321;
vector<pair<int, int>> adj[500]; // idx, cost
vector<vector<int>> parent;
vector<int> dist;
void dijkstra(int n, int src) {
parent = vector<vector<int>>(n);
dist = vector<int>(n, INF);
priority_queue<pair<int, int>> pq; // cost(-), idx
pq.emplace(0, src);
dist[src] = 0;
while (!pq.empty()) {
auto [cost, idx] = pq.top();
pq.pop();
cost = -cost;
if (dist[idx] < cost) continue;
for (auto& edge : adj[idx]) {
auto next = edge.first;
auto nextDist = cost + edge.second;
if (dist[next] > nextDist) {
dist[next] = nextDist;
pq.emplace(-nextDist, next);
parent[next].clear();
parent[next].push_back(idx);
}
else if (dist[next] == nextDist) {
parent[next].push_back(idx);
}
}
}
}
void remove_path(int n, int dst) {
vector<vector<int>> remove_list(n);
queue<int> q;
q.push(dst);
while (!q.empty()) {
int current = q.front();
q.pop();
for (auto& p : parent[current]) {
q.push(p);
remove_list[p].push_back(current);
}
}
for (int i = 0; i < n; ++i) {
for (auto& idx : remove_list[i]) {
adj[i].erase(remove_if(adj[i].begin(), adj[i].end(), [&](auto& p) {
return p.first == idx;
}), adj[i].end());
}
}
}
int main()
{
#ifndef ONLINE_JUDGE
freopen("input.txt", "r", stdin);
//freopen("output.txt", "w", stdout);
#endif
ios_base::sync_with_stdio(false);
cin.tie(nullptr), cout.tie(nullptr);
int n, m, s, d, u, v, p;
while (cin >> n >> m) {
if (n == 0 && m == 0) break;
// init
for (int i = 0; i < n; ++i)
adj[i].clear();
// input
cin >> s >> d;
for (int i = 0; i < m; ++i) {
cin >> u >> v >> p;
adj[u].emplace_back(v, p);
}
dijkstra(n, s);
int shortest = dist[d];
if (shortest == INF) {
cout << "-1\n";
continue;
}
remove_path(n, d);
while (1) {
dijkstra(n, s);
int secondary = dist[d];
if (secondary == shortest) {
remove_path(n, d);
continue;
}
else {
cout << (secondary == INF ? -1 : secondary) << '\n';
break;
}
}
}
return 0;
}반응형
'Online Judge > 백준' 카테고리의 다른 글
| [백준][C++] 14502: 연구소 (0) | 2020.08.01 |
|---|---|
| [백준][C++] 1662: 압축 (0) | 2020.08.01 |
| [백준][C++] 3182: 한동이는 공부가 하기 싫어! (0) | 2020.07.31 |
| [백준][C++] 3181: 줄임말 만들기 (0) | 2020.07.31 |
| [백준][C++] 3184: 양 (0) | 2020.07.31 |