(출처: 종만북)
다익스트라(Dijkstra, 데이크스트라) 알고리즘은 시작 정점 s부터 다른 정점까지의 최단 경로를 계산하는 알고리즘입니다.
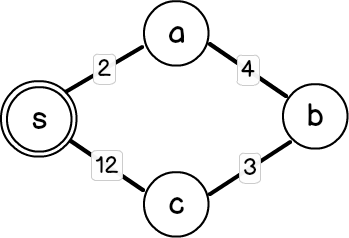
BFS(너비 우선 탐색)로는 최단경로를 찾을 수 없는데요, 그 이유는 늦게 발견한 정점을 먼저 방문할 수 없기 때문입니다.
예를 들어 Fig 1. 에서 BFS를 사용했을 때 각 노드에서 알파벳 순으로 다음 노드에 방문한다고 하면 s->a->c->b 순서로 방문하게 됩니다. 그러면 s에서 c까지의 최단경로는 사실 s-a-b-c이고 이때 거리가 9이지만 BFS로는 s-c, 거리 12의 경로만 알 수 있습니다.
다익스트라 알고리즘은 BFS와 비슷한데 큐 대신 우선순위 큐(Priority Queue)를 사용합니다. 우선순위 큐에 정점의 번호와 지금까지 찾아낸 해당 정점까지의 최단 거리를 쌍으로 넣어서 방문 단계마다 거리가 가장 가까운 정점을 방문합니다.
이 때, 각 정점까지의 최단경로가 갱신될 수 있습니다. 이미 우선순위 큐에 들어있는 정보는 어떻게 할까요? 무시하면 됩니다.
int V;
vector<pair<int, int>> adj[MAX_V]; // idx, cost
vector<int> dijkstra(int src) {
vector<int> dist(V, INF);
dist[src] = 0;
priority_queue<pair<int, int>> pq; // cost(-), idx
pq.emplace(0, src);
while (!pq.empty()) {
int cost = -pq.top().first;
int here = pq.top().second;
pq.pop();
// 지금 꺼낸것보다 더 짧은 경로가 있는 경우 무시
if (dist[here] < cost) continue;
// 인접한 노드 검사
for (auto& edge : adj[here]) {
int there = edge.first;
int nextDist = cost + edge.second;
// 더 짧은 경로 발견
if (dist[there] > nextDist) {
dist[there] = nextDist;
pq.emplace(-nextDist, there);
}
}
}
return dist;
}std::priority_queue는 기본적으로 max heap이기 때문에 cost를 음수로 변환해 넣습니다. 이렇게 하지 않으면 우선순위 큐 선언이 귀찮아집니다.
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;priority_queue의 두, 세번째 템플릿 인자는 각각 구현체(Container)와 비교자(Comparator)인데 기본값으로 std::vector<T>, std::less<typename Container::value_type>가 들어갑니다.
priority_queue를 min heap으로 바꾸려면 comparator를 less를 써줘야 하고요, 두 번째 템플릿 인자는 생략할 수 없으니 적어주게 되면 위와 같이 길게 쓸 수밖에 없습니다.
이렇게 쓰기 귀찮으니 그냥 cost를 음수로 넣어줍시다.
위 코드는 한 정점에 대한 최단 거리가 갱신될 경우 큐에 중복 원소를 넣는 방식으로 구현됐습니다. 어떤 원소 (cost, u)를 꺼냈을 때 dist[u]가 cost보다 작다면 이 원소는 중복으로 들어갔으니 무시하고 다음 원소를 꺼내면 됩니다.
다익스트라 알고리즘의 시간복잡도는 O(E log V) 입니다.
'알고리즘 > 그래프' 카테고리의 다른 글
| 플로이드 알고리즘 (Floyd-Warshall algorithm) (0) | 2020.07.03 |
|---|---|
| 벨만-포드 알고리즘(Bellman-Ford Algorithm) (0) | 2020.07.03 |
| 양방향 탐색(Bidirectional Search) (0) | 2020.05.19 |
| BFS와 BFS 스패닝 트리 구현 (0) | 2020.05.18 |
| 무향 그래프에서 DFS를 이용해 오일러 회로 찾기 (0) | 2020.05.13 |