Lazy Propagation (Segment Tree)

Segment Tree에서 Lazy Propagation(레이지 프로파게이션, 늦은 전파?)에 대해 알아보겠습니다

세그먼트 트리 중 RSQ(Range Sum Query) segment tree를 예로 들어보겠습니다.

 

 

Lazy Propagation 개념 및 예제

Fig 1. RSQ를 위한 세그먼트 트리 예시

배열이 주어지고, 배열에서 아래 두 연산을 수행해야 하는 문제가 있습니다. (ex. 10999: 구간 합 구하기 2)

• Query: [l, r]의 합을 출력하기
• Update: [l, r]의 범위에 a라는 값을 더하기
  • arr[l] += a, arr[l+1] += a, ..., arr[r] += a

세그먼트 트리를 쓰면 Query는 O(lgN)의 시간복잡도를 가집니다.

Update가 문제인데, 세그먼트 트리에서 수 하나를 변경하려면 O(lgN)의 시간이 걸리니, l-r+1개를 업데이트할 때는 O(NlgN)의 시간이 걸립니다. update를 여러번 하면 시간초과가 나올 겁니다.

 

Fig 2. [0, 4]의 범위에 1을 더하는 update_range를 실행한 모습

Lazy Propagation은 구간 업데이트를 할 때, 당장은 리프 노드까지 이어지는 모든 노드를 업데이트 할 필요가 없다는 것에 아이디어를 착안합니다.

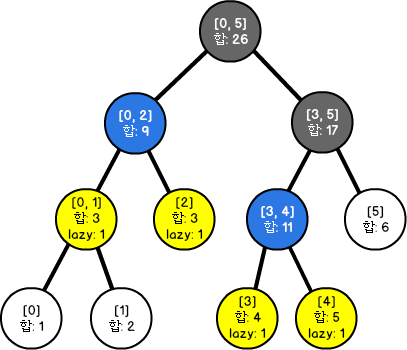
즉 [l, r]에 a씩 더하는 update 쿼리가 들어오면, 노드 표현 범위에 [l, r]에 완전히 포함되는 노드 중 부모 노드와 루트부터 부모노드까지의 노드 값만 업데이트 합니다. 업데이트한 노드의 자식 노드들은 아직 업데이트를 하지 않고 미뤄둡니다

업데이트 한 노드의 자식 노드의 업데이트는 나중에 필요할 때 하기로 하고, 그 값을 lazy[i]에 적어둡니다.

Fig 2.를 보시면 [l, r]에 포함되는 노드의 부모 노드인 파란색 노드와 루트부터 파란색 노드까지 방문하는 회색 노드만 합의 값이 업데이트 된 것을 확인할 수 있습니다.

 

Fig 3. [1]번 인덱스 query가 들어왔을 때 propagation을 진행한 모습

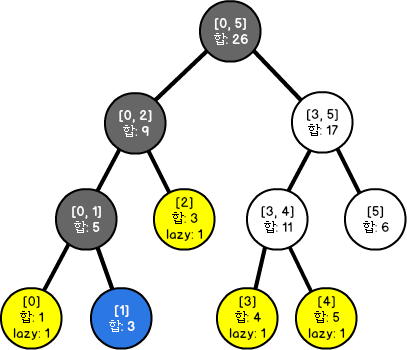
이후에는 항상 어떤 노드를 방문할 때마다 lazy 값이 있는지 검사하고, lazy 값이 0이 아니라면 현재 노드에 해당하는 값을 노드의 표현 구간이 [start, end]라 할 때 (end-start+1)를 곱해서 더한 다음, 자식 노드에 lazy 값을 물려줘야 합니다. 이 과정을 propagation이라고 합니다.

propagation을 필요할 때, 나중에(lazy) 하기 때문에 lazy propagation이라고 합니다.

 

Lazy Propagation을 사용하면 범위 update 쿼리도 O(lgN)에 처리할 수 있다는 이점이 있습니다.

단점이라면 세그먼트 트리 만들때 사용한 배열과 동일한 크기의 lazy 배열이 필요해 메모리를 좀 더 쓴다는 겁니다.

 

 

소스코드

/////////////////////////////////////////////////////////////////////////
// RSQ with Lazy Propagation
template <typename T>
struct RSQ {
	int n;
	vector<long long> rangeSum;
	vector<long long> lazy;

	RSQ(const vector<T>& arr) {
		n = arr.size();
		rangeSum.resize(n * 4);
		lazy.resize(n * 4);
		init(arr, 0, n - 1, 1);
	}

	// arr[left, right]를 초기화
	T init(const vector<T>& arr, int left, int right, int node) {
		if (left == right)
			return rangeSum[node] = arr[left];

		int mid = (left + right) / 2;
		T left_sum = init(arr, left, mid, node * 2);
		T right_sum = init(arr, mid + 1, right, node * 2 + 1);

		return rangeSum[node] = left_sum + right_sum;
	}

	// node의 표현 범위 arr[nodeLeft, nodeRight]가 주어졌을 때
	// 쿼리의 arr[left, right]의 교집합 sum을 구함
	T query(int left, int right,
		int node, int nodeLeft, int nodeRight) {
		// lazy propagation
		propagate(node, nodeLeft, nodeRight);

		// 두 구간이 겹치지 않은 경우
		if (right < nodeLeft || nodeRight < left) return 0;

		// node의 표현 범위가 query에 완전히 포함되는 경우
		if (left <= nodeLeft && nodeRight <= right) return rangeSum[node];

		int mid = (nodeLeft + nodeRight) / 2;
		return query(left, right, node * 2, nodeLeft, mid) +
			query(left, right, node * 2 + 1, mid + 1, nodeRight);
	}

	T query(int left, int right) {
		return query(left, right, 1, 0, n - 1);
	}

	void propagate(int node, int nodeLeft, int nodeRight) {
		if (lazy[node] != 0) {
			rangeSum[node] += (nodeRight - nodeLeft + 1) * lazy[node];
			// leaf가 아니면
			if (nodeLeft != nodeRight) {
				lazy[node * 2] += lazy[node];
				lazy[node * 2 + 1] += lazy[node];
			}
			lazy[node] = 0;
		}
	}

	// [left, right]에 val을 더함 (lazy propagation)
	T update_range(int left, int right, T val,
		int node, int nodeLeft, int nodeRight) {
		// lazy propagation
		propagate(node, nodeLeft, nodeRight);

		// 두 구간이 겹치지 않는 경우
		if (right < nodeLeft || nodeRight < left) return rangeSum[node];

		// node 표현범위에 [left, right]가 완전히 포함될 경우 자식 노드는 lazy 배열에 넣음
		if (left <= nodeLeft && nodeRight <= right) {
			rangeSum[node] += val * (nodeRight-nodeLeft+1);
			if (nodeLeft != nodeRight) {
				lazy[node * 2] += val;
				lazy[node * 2 + 1] += val;
			}
			return rangeSum[node];
		}

		int mid = (nodeLeft + nodeRight) / 2;
		return rangeSum[node] = update_range(left, right, val, node*2, nodeLeft, mid) +
			update_range(left, right, val, node*2+1, mid+1, nodeRight);
	}

	// [left, right]에 val을 더함 (lazy propagation)
	T update_range(int left, int right, T val) {
		return update_range(left, right, val, 1, 0, n-1);
	}
};

소스입니다.

update를 update_range로 바꿨고, propagate 메소드가 추가됐습니다.

query와 update_range를 진행할 때 각 노드에서 propagate 메소드를 호출합니다. 노드 표현 범위에 update 쿼리 범위가 완전히 포함되는 경우(Fig. 2,3에서 파란색 노드) 노드의 값을 업데이트 하고 자식 노드의 lazy 값을 추가합니다.