문제 링크: https://www.acmicpc.net/problem/17197
소가 N마리 있고 (x, y) 평면에 소가 존재합니다. 이때 소가 그룹(moo network)으로 나뉘어져 있는데, 1개 이상의 그룹을 포함하는 울타리의 최소 둘레 길이를 구하면 됩니다.
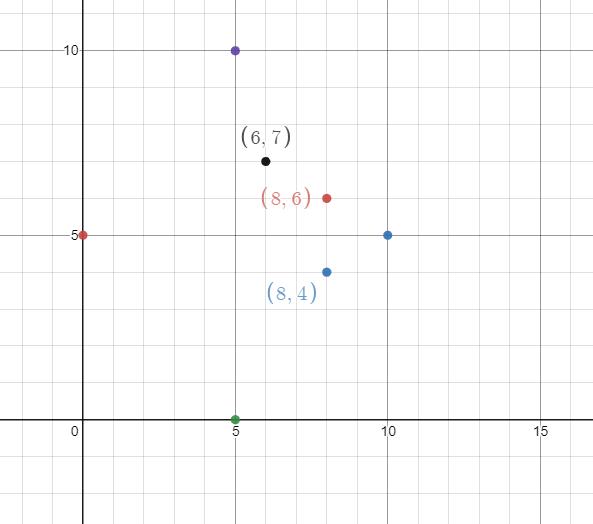
예를 들어 예제에서는 Fig 1.처럼 (6,7) (8,6) (8,4)의 소가 하나의 그룹이고 이 소들을 포함하는 울타리를 치려면 왼쪽 아래가 (6, 4) 오른쪽 위가 (8, 7)인 직사각형이 되고, 이 직사각형의 둘레의 길이는 10이고 문제의 정답이 됩니다.
disjoint set 또는 bfs를 사용하면 되는데요, 소를 몇개의 그룹으로 분할할 때 disjoint set, bfs를 사용한 뒤 각각의 그룹에 대해서 그 그룹을 포함할 수 있는 울타리의 최소 길이를 구해 이 길이들의 최소값을 구합니다.
울타리의 최소 길이는 2*(두 점 사이 x좌표 차이의 최대값 + 두 점 사이 y좌표 차이의 최대값) 입니다.
\[ perimeter(A) = 2 \times \biggl (
max \Bigl ( \Bigl \{ |x_i - x_j| \Bigm | i, j \in A \Bigr \} \Bigr ) + max \Bigl ( \Bigl \{ |y_k - y_q| \Bigm | k, q \in A \Bigr \} \Bigr )
\biggr ) \]
식으로 나타내면 대충 위와 같겠네요. 소 그룹 A에 대한 울타리 둘레의 최소 길이를 나타낸 식입니다.
#include <bits/stdc++.h>
using namespace std;
const int INF = 987654321;
vector<int> parent;
vector<tuple<int, int, int, int>> vp; //max <y, x>, min <y, x>
void init(int sz) {
parent.resize(sz);
for (int i = 0; i < sz; ++i)
parent[i] = i;
}
int find(int u) {
if (u == parent[u]) return u;
return parent[u] = find(parent[u]);
}
void merge(int u, int v) {
u = find(u), v = find(v);
if (u == v) return;
parent[u] = v;
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(nullptr);
int n, m;
cin >> n >> m;
init(n);
vp.resize(n);
int u, v;
for (int i = 0; i < n; ++i) {
cin >> u >> v;
vp[i] = { v, u, v, u };
}
for (int i = 0; i < m; ++i) {
cin >> u >> v;
--u, --v;
u = find(u), v = find(v);
if (u != v) {
vp[v] = make_tuple(
max(get<0>(vp[u]), get<0>(vp[v])),
max(get<1>(vp[u]), get<1>(vp[v])),
min(get<2>(vp[u]), get<2>(vp[v])),
min(get<3>(vp[u]), get<3>(vp[v]))
);
merge(u, v);
}
}
int min_perimeter = INF;
for (int i = 0; i < n; ++i) {
if (i != find(i)) continue;
auto& [max_y, max_x, min_y, min_x] = vp[i];
min_perimeter = min(min_perimeter, 2*(abs(max_y-min_y)+abs(max_x-min_x)));
}
cout << min_perimeter << '\n';
return 0;
}각 그룹의 x, y좌표의 최대, 최소를 저장하기 위한 배열을 만들어서 활용했습니다.
'Online Judge > 백준' 카테고리의 다른 글
| [백준][C++] 10888: 두 섬간의 이동 (0) | 2020.06.02 |
|---|---|
| [백준][C++] 10216: Count Circle Groups (0) | 2020.06.01 |
| [백준][C++] 4358: 생태학 (0) | 2020.05.30 |
| [백준][C++] 12790: Mini Fantasy War (0) | 2020.05.29 |
| [백준][C++] 17352: 여러분의 다리가 되어드리겠습니다! (0) | 2020.05.28 |