위상 정렬(Topological Sort)이란 의존성 있는 작업이 주어질 때, 작업을 어떤 순서로 수행해야 하는지 계산하는 방법입니다.

의존성이 있는 작업의 예로는 대학교 과목의 선수과목을 예로 들 수 있습니다. Fig 1.를 예로 들면 'IoT디지털시스템'을 수강하려면 '컴퓨터구조'를 먼저 수강해야 하고, '컴퓨터구조'를 수강하려면 논리회로를 먼저 수강해야 합니다.
작업간의 의존 관계를 간선으로 표현한 그래프를 의존성 그래프(dependency graph)라고 합니다. 작업 v가 u에 의존한다면 의존성 그래프는 간선 (u, v)를 포함하게 됩니다.

의존성 그래프의 특징은 그래프에 사이클이 존재하지 않는다는 겁니다. 이 그래프는 사이클 없는 방향 그래프, DAG(Directed Acyclic Graph)라고도 부릅니다.

의존성 그래프의 정점들을 일렬로 늘어놓고, 왼쪽부터 하나씩 수행한다고 했을 때, 모든 의존성이 만족되려면 모든 간선이 왼쪽에서 오른쪽으로만 가야 합니다.
Fig 3.은 정점을 재배열 한 두가지 예시입니다. 위 그래프의 모든 간선은 왼쪽에서 오른쪽으로 가니 적절한 위상정렬 결과이지만, 아래 그래프에서는 빨간색으로 칠한 간선이 오른쪽에서 왼쪽으로 가기 때문에 적절한 위상정렬의 결과가 아닙니다.
위상정렬 구현방법은 보통 두 가지 방법이 있는데 진입차수(In-degree, 인-디그리)를 이용한 방법과 DFS를 이용한 방법이 있습니다.
진입차수(Indegree)를 이용한 위상 정렬 구현
(작성중)
DFS를 이용한 위상 정렬 구현
dfs를 수행할 때 dfs 함수가 종료될 때마다 현재 정점의 번호를 기록하고, 모든 dfs 함수가 종료될 때 기록된 순서를 뒤집으면 위상 정렬의 결과를 얻을 수 있습니다.
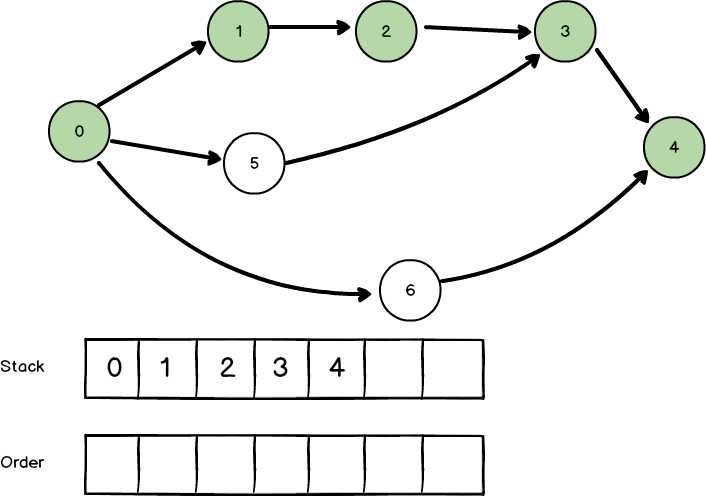
위와 같은 DAG가 있다고 했을 때 DFS를 수행해보겠습니다.
0 -> 1 -> 2 -> 3 -> 4까지 진행합니다. 4번 노드의 다음 노드가 없으니 order에 추가하고 종료합니다.

동일한 방식으로 3, 2, 1번 노드도 order에 추가하고 종료합니다. 다음으로 5번 노드를 진행하는데 3번 노드가 이미 방문한 노드이니 order에 추가하고 종료합니다.

6번 노드도 마찬가지로 다음 노드인 4번 노드가 이미 방문한 노드이기 때문에 order에 추가하고 종료합니다.
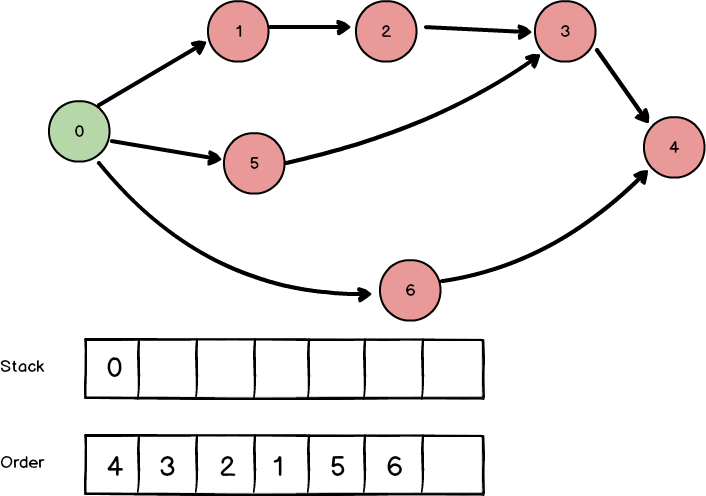
0번 노드로 다시 돌아와서 방문하지 않은 다음 노드가 없으니 order에 추가하고 종료합니다
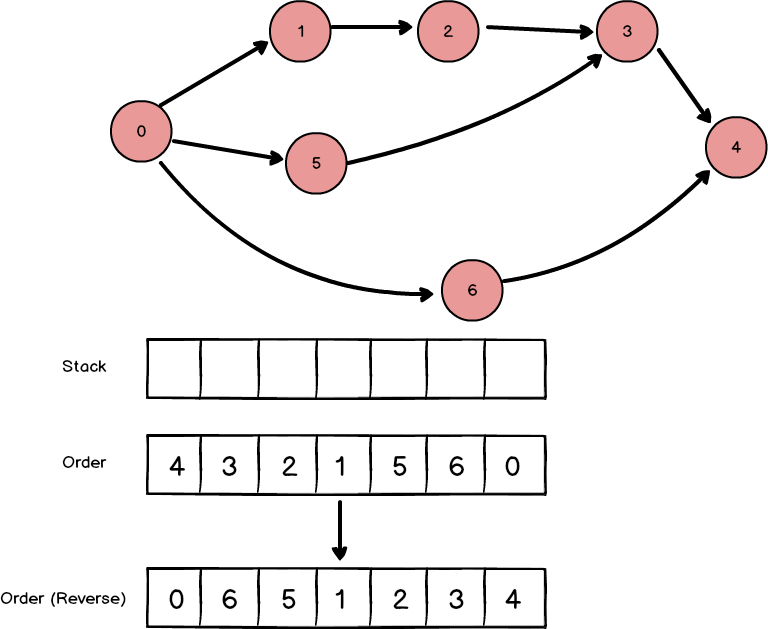
모든 노드를 방문했습니다. order를 뒤집으면 위상정렬한 순서가 됩니다. 처음부터 order의 앞에 추가할 수도 있지만, 배열의 맨 앞에 추가하는 연산은 비효율적이기 때문에 마지막에 한꺼번에 뒤집었습니다.
그래프가 두 개 이상의 컴포넌트에 나뉘어있는 경우(e.g. Fig. 2)를 위해 모든 노드에 대해 dfs를 수행하셔야 합니다.
#pragma GCC optimize ("Ofast")
#pragma GCC target("sse,sse2,sse3,ssse3,sse4,avx,avx2")
#define _CRT_SECURE_NO_WARNINGS
#include <bits/stdc++.h>
using namespace std;
vector<vector<int> > graph;
vector<int> visited, order;
int n, m;
void dfs(int current) {
visited[current] = 1;
for (auto& next : graph[current])
if (!visited[next])
dfs(next);
order.push_back(current);
}
vector<int> topologicalSort() {
visited = vector<int>(n, 0);
for (int i = 0; i < n; ++i)
if (!visited[i])
dfs(i);
reverse(order.begin(), order.end());
return order;
}
int main()
{
#ifndef ONLINE_JUDGE
freopen("input.txt", "r", stdin);
//freopen("output.txt", "w", stdout);
#endif
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(nullptr);
cin >> n >> m;
graph.resize(n);
while (m--) {
int a, b;
cin >> a >> b;
--a; --b;
graph[a].push_back(b);
}
auto ord = topologicalSort();
for (auto& o : ord)
cout << o+1 << ' ';
cout << '\n';
return 0;
}백준 2252: 줄세우기 문제를 dfs를 이용한 위상정렬로 푼 소스입니다.
'알고리즘 > 그래프' 카테고리의 다른 글
| 양방향 탐색(Bidirectional Search) (0) | 2020.05.19 |
|---|---|
| BFS와 BFS 스패닝 트리 구현 (0) | 2020.05.18 |
| 무향 그래프에서 DFS를 이용해 오일러 회로 찾기 (0) | 2020.05.13 |
| 해밀턴 경로(Hamiltonian Path), 해밀턴 회로(Hamiltonian Circuit) (0) | 2020.04.06 |
| 오일러 회로(Eulerian Circuit), 오일러 트레일(Eulerian Trail) (0) | 2020.04.04 |