문제 링크: https://www.acmicpc.net/problem/1199
저번 게시물에서 오일러 회로와 경로에 대해 간단하게 설명했습니다.
이 문제는 오일러 회로 기본 문제입니다. 입력으로 그래프를 만들고, degree를 확인해 전부 짝수인지 확인합니다. 홀수면 오일러 회로가 아니니 -1을 출력합니다.
오일러 회로는 DFS로 구하면 됩니다. 모든 간선을 다 방문했을 때가 base case가 될 겁니다.
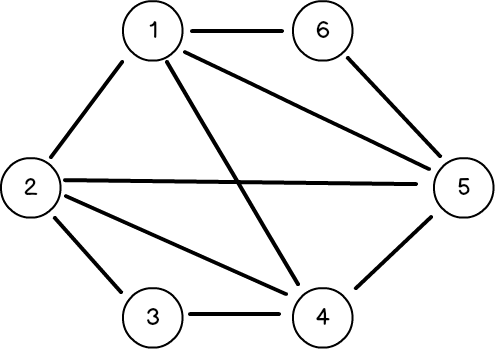
예제입니다. 모든 노드의 차수가 짝수이므로 오일러 회로고, 예제 출력은 1 2 3 4 1 5 2 4 5 6 1 입니다.
#define _CRT_SECURE_NO_WARNINGS
#include <bits/stdc++.h>
using namespace std;
int n; //정점의 수
int num_of_edges;
int graph[1000][1000];
int degree[1000];
void dfs(int node, vector<int>& visited) {
if (!num_of_edges) {
for (auto& c : visited)
cout << c+1 << ' ';
exit(0);
}
for (int i = 0; i < n; ++i) {
if (graph[node][i]) {
--graph[node][i];
--graph[i][node];
--num_of_edges;
visited.push_back(i);
dfs(i, visited);
++graph[node][i];
++graph[i][node];
++num_of_edges;
visited.pop_back();
}
}
}
int main()
{
#ifndef ONLINE_JUDGE
freopen("input.txt", "r", stdin);
#endif
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cin >> n;
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
cin >> graph[i][j];
if (graph[i][j]) {
degree[i] += graph[i][j];
degree[j] += graph[i][j];
num_of_edges += graph[i][j];
}
}
}
num_of_edges /= 2;
// Eulerian circuit -> 모든 정점이 짝수점이어야함
bool is_eulerian_circuit = true;
for (int i = 0; i < n; ++i) {
degree[i] /= 2; //non-directed이므로
if (degree[i] % 2) { //홀수점인 경우
is_eulerian_circuit = false;
break;
}
}
if (!is_eulerian_circuit) {
cout << -1;
return 0;
}
vector<int> v{ 0 };
dfs(0, v);
return 0;
}두 노드 사이에 간선이 여러개 올 수 있는 점을 감안해서 작성해야 합니다.
반응형
'Online Judge > 백준' 카테고리의 다른 글
| [백준][C++] 17471: 게리맨더링 (0) | 2020.04.08 |
|---|---|
| [백준][C++] 1107: 리모컨 (0) | 2020.04.07 |
| [백준][C++] 15686: 치킨 배달 (0) | 2020.03.31 |
| [백준][C++] 15685: 드래곤 커브 (0) | 2020.03.28 |
| [백준][C++] 14500: 테트로미노 (0) | 2020.03.26 |